We will first illustrate the Montessus’s theorem with the function:
where . This function has two poles at
and
.
The corresponding Maclaurin series is:
The corresponding approximant is (calculations were made according to the linear systems presented in this post):
We see that, in this case, if we set (the total number of poles) we recover the original function since
. The graphs of the
,
and the corresponding Maclaurin series are presented in the figure below.
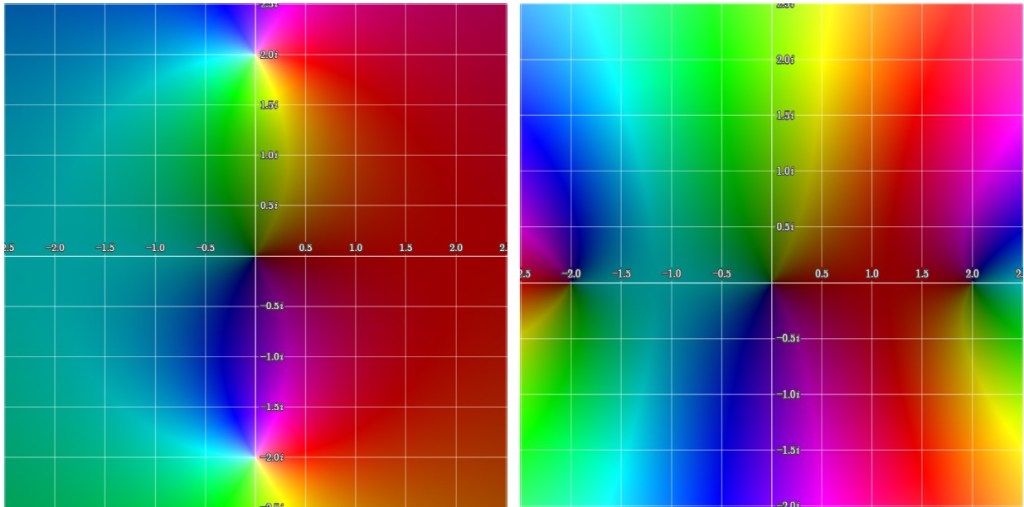
Left, graph of
and its corresponding . Right, graph of the Maclaurin series
in the complex -plane. The poles at
and
are clearly visible on the left picture. Hue and brightness are used to display phase and magnitude, respectively.
The Montessus’s theorem is also illustrated in the figures below for the function tan(z).
and
of the function. The improvement of the approximation between
and
is visible on the figures.
Graph of tan(z):
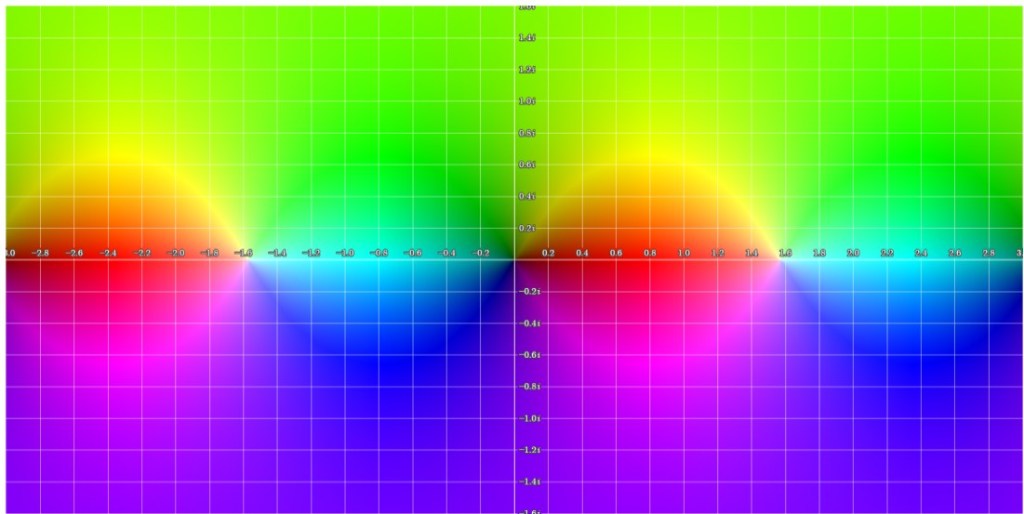
Graphs of the P(2,2) (left) and P(4,2) (right) of tan(z):


Pictures were produced using: Samuel Jinglian, 2018. “Complex Function Plotter.” https://samuelj.li/complex-function-plotter/.
Leave a comment