Padé approximants

We would like to represent functions using continued fractions (similarly as we did for numbers). For example, a well-known continued fraction representing $tan(x)$ is:

$\displaystyle tan(x) = \frac{x}{1 - \frac{x^2}{3 - \frac{x^2}{5 - \frac{x^2}{7 - \cdots}}}}$

Continued fractions like this one typically have a bigger definition domain compared to the corresponding Taylor series. This is illustrated graphically in figure 1 and figure 2.

The continued fraction representation of a function seems a promising approach since the radius of convergence ‘seems’ at a first glance much bigger and the approximation ‘looks’ much better (i.e. converging faster) than for Taylor and Maclaurin series. We will illustrate these statements.

In order to make some progress in the construction of continued fractions corresponding to functions, we’ll start by defining the following rational functions, which will prove to have interesting properties in their own right:

$\displaystyle P(1,1) := \frac{A_0 + A_1 x}{1 + B_1 x}$

$\displaystyle P(2,1) := \frac{A_0 + A_1 x + A_2 x^2}{1 + B_1 x}$

$\displaystyle P(2,2) := \frac{A_0 + A_1 x + A_2 x^2}{1 + B_1 x + B_2 x^2}$

$\displaystyle \cdots$

$\displaystyle P(m,n) := \frac{A_0 + A_1 x + A_2 x^2 + \cdots + A_m x^m}{1 + B_1 x + B_2 x^2 + \cdots + B_n x^n}$

Using the definitions above we present some examples using the first terms of the Maclaurin series of $tan(x)$ :

$\displaystyle \frac{A_0 + A_1 x + A_2 x^2}{1 + B_1 x + B_2 x^2} = x + \frac{1}{3} x^3$

$\displaystyle A_0 + A_1 x + A_2 x^2 = (x + \frac{1}{3} x^3) (1 + B_1 x + B_2 x^2)$

$\displaystyle A_0 + A_1 x + A_2 x^2 = x + B_1 x^2 + B_2 x^3 + \frac{1}{3} x^3 + \frac{1}{3} B_1 x^4 + \frac{1}{3} B_2 x^5$

$\displaystyle A_0 + A_1 x + A_2 x^2 = x + B_1 x^2 + \left(B_2 + \frac{1}{3}\right) x^3 + \frac{1}{3} B_1 x^4 + \frac{1}{3} B_2 x^5$

In the example above we are considering a $P(2,2)$ rational function. So we consider up to 2 + 2 = 4 as the maximum degree we would like to consider for further computations. The equation above becomes:

$\displaystyle A_0 + A_1 x + A_2 x^2 = x + B_1 x^2 + \left(B_2 + \frac{1}{3}\right) x^3 + \frac{1}{3} B_1 x^4$

Comparing the coefficients of both sides we obtain:

$\displaystyle A_0 = 0 \quad \text{and} \quad B_2 + \frac{1}{3} = 0$

$\displaystyle A_1 = 1 \quad \text{and} \quad \frac{1}{3} B_1 = 0$

$\displaystyle A_2 = B_1$

Solving the set of equations above gives:

$\displaystyle A_0 = 0, \ A_1 = 1, \ A_2 = 0, \ B_1 = 0, \ B_2 = -\frac{1}{3}$

$\displaystyle \implies P(2,2) := \frac{A_0 + A_1 x + A_2 x^2}{1 + B_1 x + B_2 x^2} = \frac{x}{1 - \frac{1}{3} x^2}$

This is clearly the first term of the continued fraction of $tan(x)$ as shown above.

$P(m,n)$ as defined above are called Padé approximants. A Padé approximant is the “best” approximation of a function near a specific point by a rational function of given order. We also have convergence beyond the radius of convergence of the corresponding series.

Let’s calculate the $P(1,2)$ corresponding to the first terms of the Maclaurin series of $tan(x)$ . 1 + 2 = 3 implies that we have to consider the Taylor series up to degree 3.

$\displaystyle \frac{A_0 + A_1 x}{1 + B_1 x + B_2 x^2} = x + \frac{1}{3} x^3$

$\displaystyle A_0 + A_1 x = (x + \frac{1}{3} x^3) (1 + B_1 x + B_2 x^2)$

$\displaystyle A_0 + A_1 x = x + B_1 x^2 + B_2 x^3 + \frac{1}{3} x^3 + \frac{1}{3} B_1 x^4 + \frac{1}{3} B_2 x^5$

$\displaystyle A_0 + A_1 x = x + B_1 x^2 + \left(B_2 + \frac{1}{3}\right) x^3 + \frac{1}{3} B_1 x^4 + \frac{1}{3} B_2 x^5$

Keeping only degrees up to 3:

$\displaystyle A_0 + A_1 x = x + B_1 x^2 + \left(B_2 + \frac{1}{3}\right) x^3$

Comparing the coefficients of both sides we obtain:

$\displaystyle A_0 = 0 \quad \text{and} \quad B_1 = 0$

$\displaystyle A_1 = 1 \quad \text{and} \quad B_2 + \frac{1}{3} = 0 \implies B_2 = -\frac{1}{3}$

$\displaystyle \implies P(1,2) := \frac{A_0 + A_1 x}{1 + B_1 x + B_2 x^2} = \frac{x}{1 - \frac{1}{3} x^2}$

We observe that (in this case):

$\displaystyle P(1,2) = P(2,2)$

Now we calculate the $P(3,3)$ corresponding to the first terms of the Maclaurin series of $tan(x)$ . 3 + 3 = 6 implies that we have to consider the Taylor series up to degree 5:

$\displaystyle \frac{A_0 + A_1 x + A_2 x^2 + A_3 x^3}{1 + B_1 x + B_2 x^2 + B_3 x^3} = x + \frac{1}{3} x^3 + \frac{2}{15} x^5$

$\displaystyle A_0 + A_1 x + A_2 x^2 + A_3 x^3 = (x + \frac{1}{3} x^3 + \frac{2}{15} x^5) (1 + B_1 x + B_2 x^2 + B_3 x^3)$

$\displaystyle A_0 + A_1 x + A_2 x^2 + A_3 x^3 = x + B_1 x^2 + B_2 x^3 + B_3 x^4 + \frac{1}{3} x^3 + \frac{1}{3} B_1 x^4 + \frac{1}{3} B_2 x^5 + \frac{1}{3} B_3 x^6 + \frac{2}{15} x^5 + \frac{2}{15} B_1 x^6 + \frac{2}{15} B_2 x^7 + \frac{2}{15} B_3 x^8$

$\displaystyle A_0 + A_1 x + A_2 x^2 + A_3 x^3 = x + B_1 x^2 + \left(B_2 + \frac{1}{3}\right) x^3 + \left(B_3 + \frac{1}{3} B_1\right) x^4 + \left(\frac{1}{3} B_2 + \frac{2}{15}\right) x^5 + \left(\frac{1}{3} B_3 + \frac{2}{15} B_1\right) x^6 + \frac{2}{15} B_2 x^7 + \frac{2}{15} B_3 x^8$

Keeping only degrees up to 6:

This implies:

$\displaystyle A_0 = 0 \quad \text{and} \quad B_3 + \frac{1}{3} B_1 = 0$

$\displaystyle A_1 = 1 \quad \text{and} \quad \frac{1}{3} B_2 + \frac{2}{15} = 0$

$\displaystyle A_2 = B_1 \quad \text{and} \quad \frac{1}{3} B_3 + \frac{2}{15} B_1 = 0$

$\displaystyle A_3 = B_2 + \frac{1}{3}$

Solving the set of equations above gives:

$\displaystyle A_0 = 0, \ A_1 = 1, \ A_2 = 0, \ A_3 = -\frac{1}{15}, \ B_1 = 0, \ B_2 = -\frac{2}{5}, \ B_3 = 0$

$\displaystyle \implies P(3,3) := \frac{A_0 + A_1 x + A_2 x^2 + A_3 x^3}{1 + B_1 x + B_2 x^2 + B_3 x^3} = \frac{x - \frac{1}{15} x^3}{1 - \frac{6}{15} x^2}$

Now consider the first terms of the continued fraction of $tan(x)$ :

$\displaystyle \frac{x}{1 - \frac{x^2}{3 - \frac{x^2}{5}}} = \frac{x}{1 - \frac{x^2}{\frac{15 - x^2}{5}}} = \frac{x}{1 - \frac{5 x^2}{15 - x^2}} = \frac{15 x - x^3}{15 - x^2 - 5 x^2} = \frac{15 x - x^3}{15 - 6 x^2}$

$\displaystyle \implies P(3,3) = \frac{x - \frac{1}{15} x^3}{1 - \frac{6}{15} x^2} = \frac{x}{1 - \frac{x^2}{3 - \frac{x^2}{5}}}$

Therefore, the $P(1,1)$ , $P(2,2)$ and $P(3,3)$ Padé approximants (see fig. 3, 4 and 5) of $tan(x)$ are equivalent to the first terms of its continued fraction as presented above.

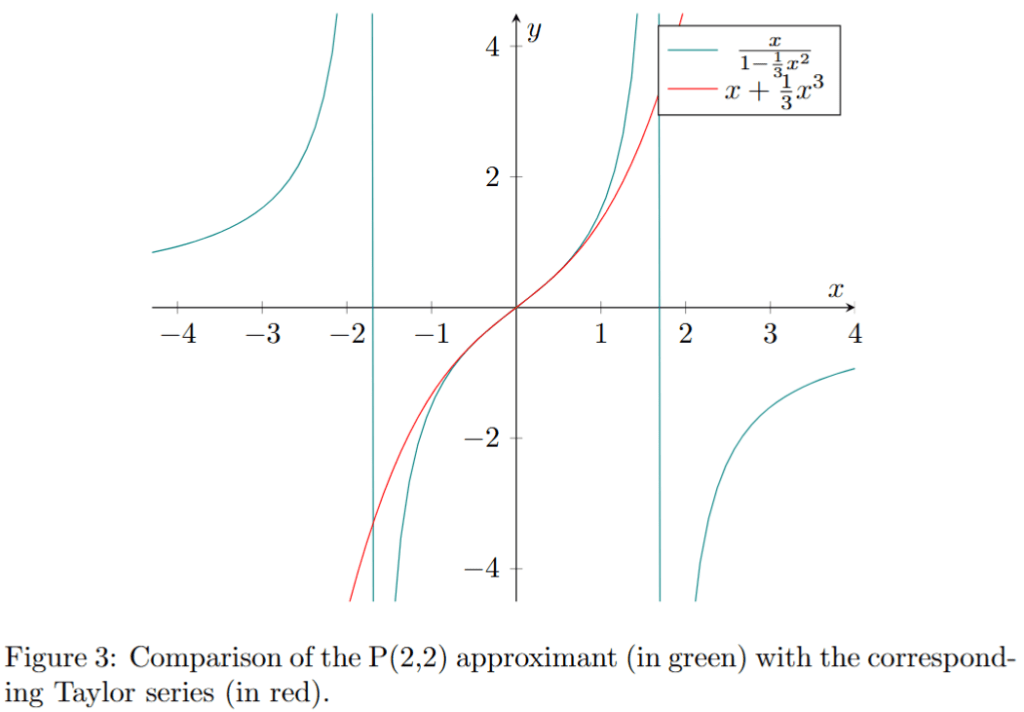
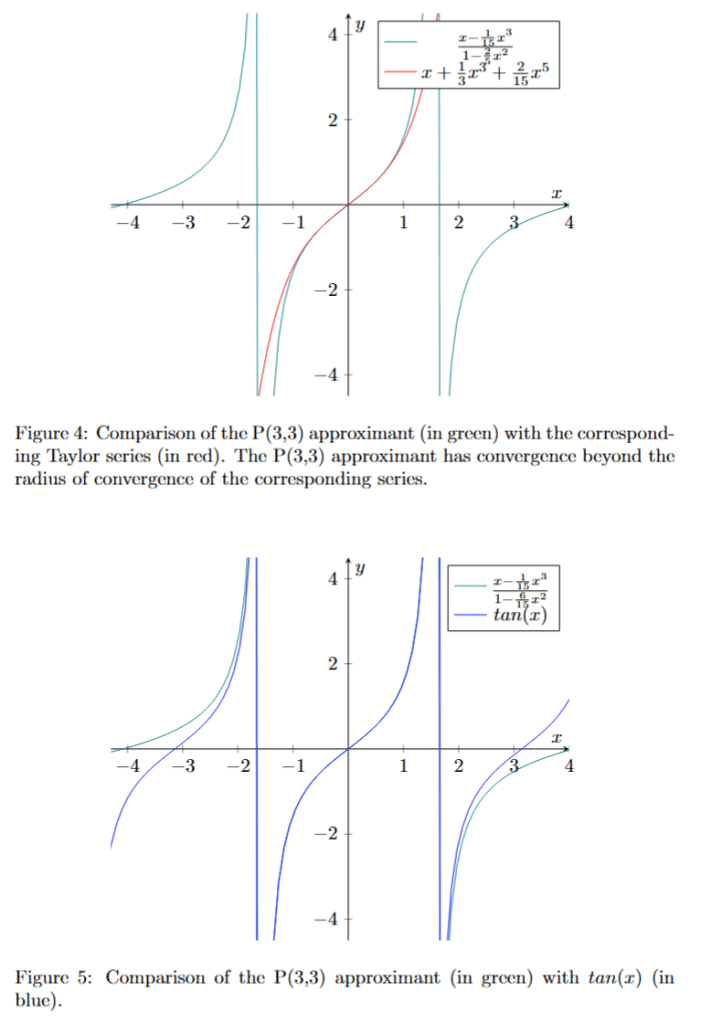
The results above about $tan(x)$ suggest that a “Padé transformation” (i.e. converting a series into a rational function using the procedure described above) of a divergent Maclaurin and Taylor series is converging beyond the radius of convergence of the Maclaurin series.

This gives hope for the use of divergent series as often encountered in perturbation theory.

We would like to calculate the $P(m,n)$ of $exp(x)$ . First, we would like to calculate $P(1,1)$ . We, therefore, consider the Maclaurin series of $exp(x)$ up to 1 + 1 = 2 degrees: