Approximaths

Author: approximaths

  • Padé approximants: Possible application

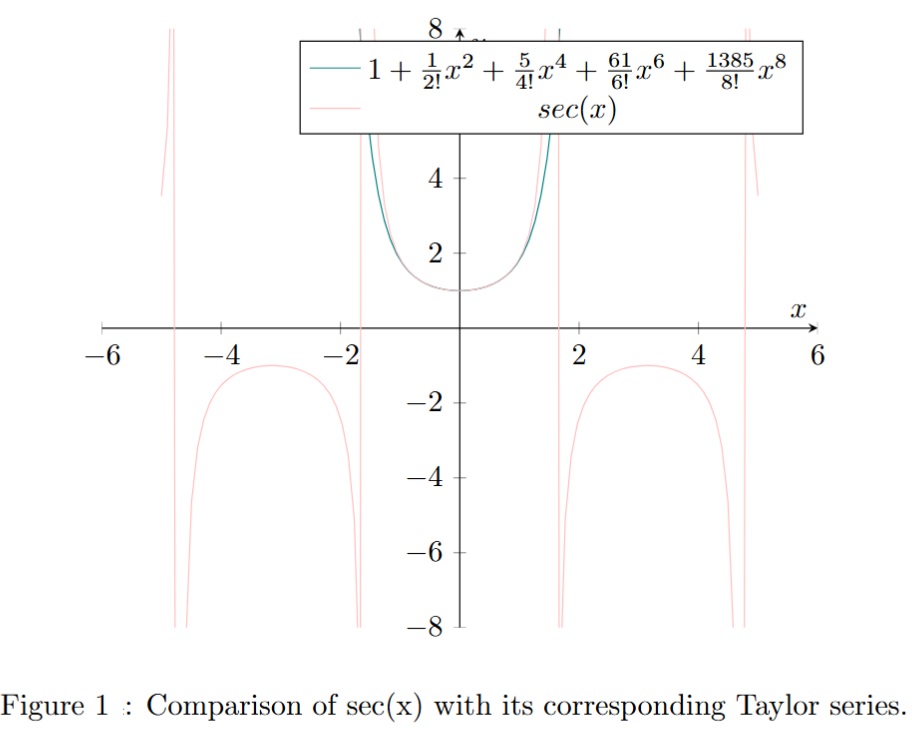
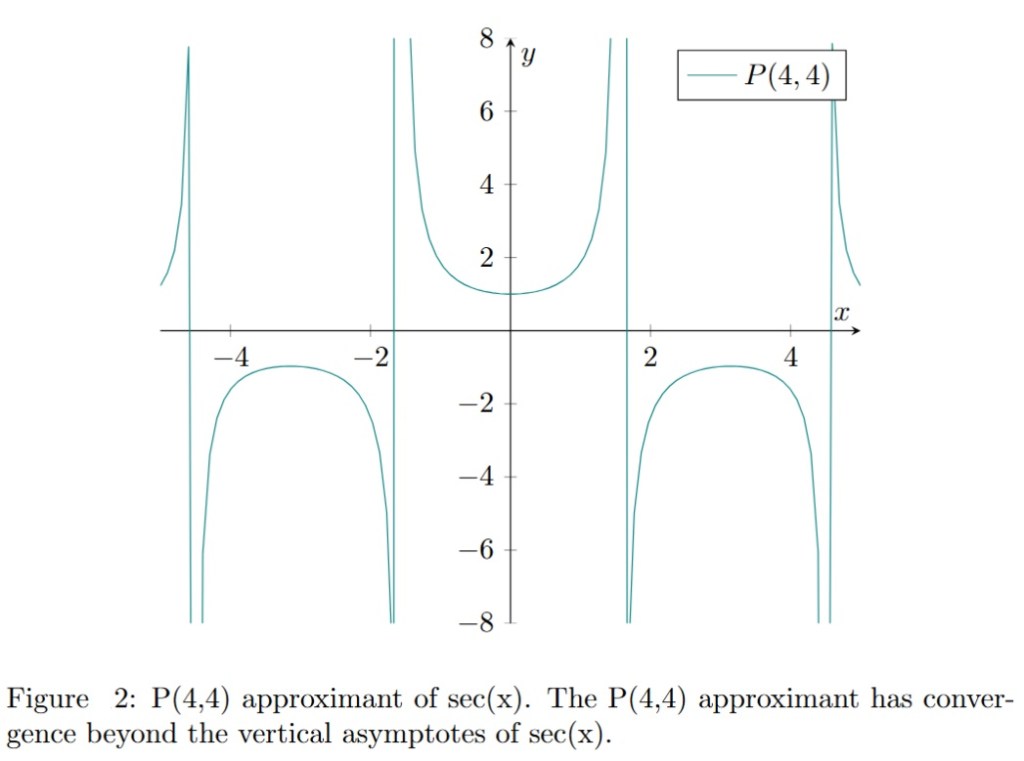
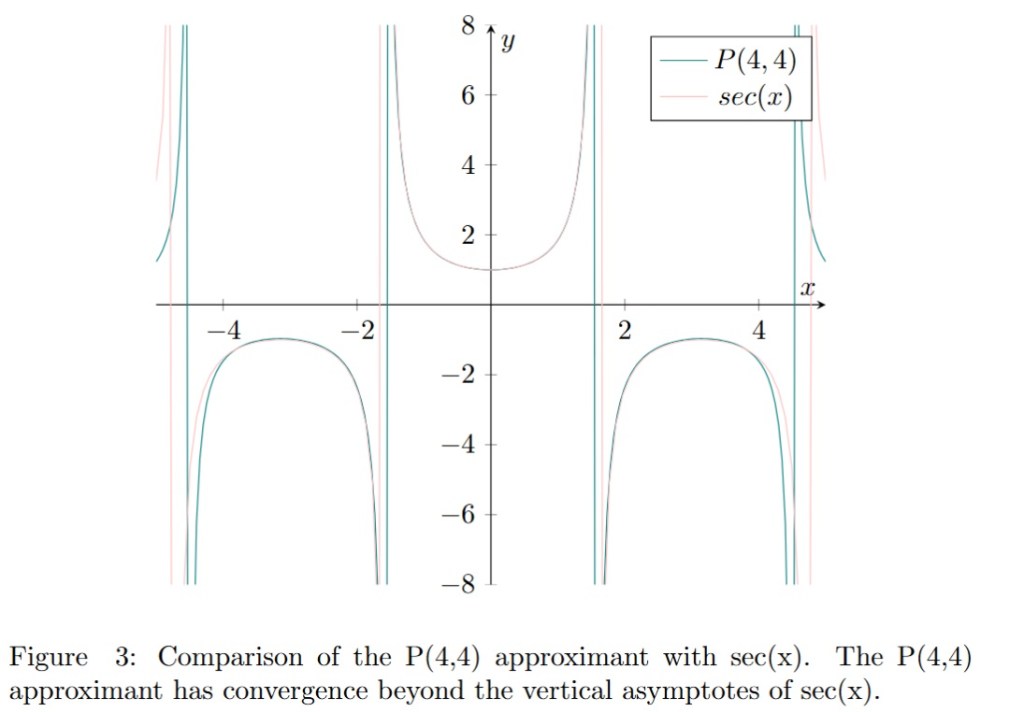
    The basic idea beyond Padé approximants is to construct a rational fraction whose Taylor series expansion near the origin coincides with that of a given function up to the maximum order. In the previous sections we introduced Padé approximants P(m,n) and a procedure to calculate their coefficients by solving 2 systems of linear equations sequentially (see this post).

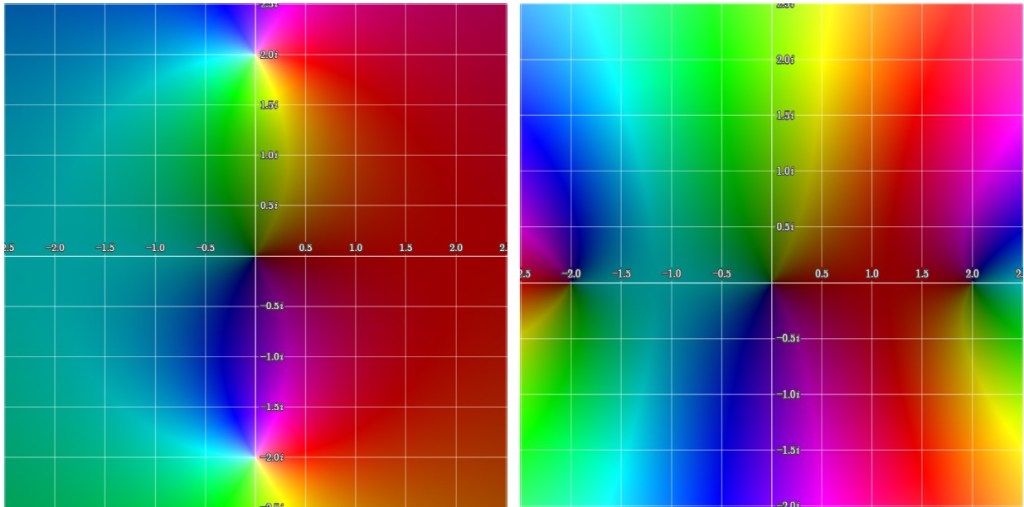
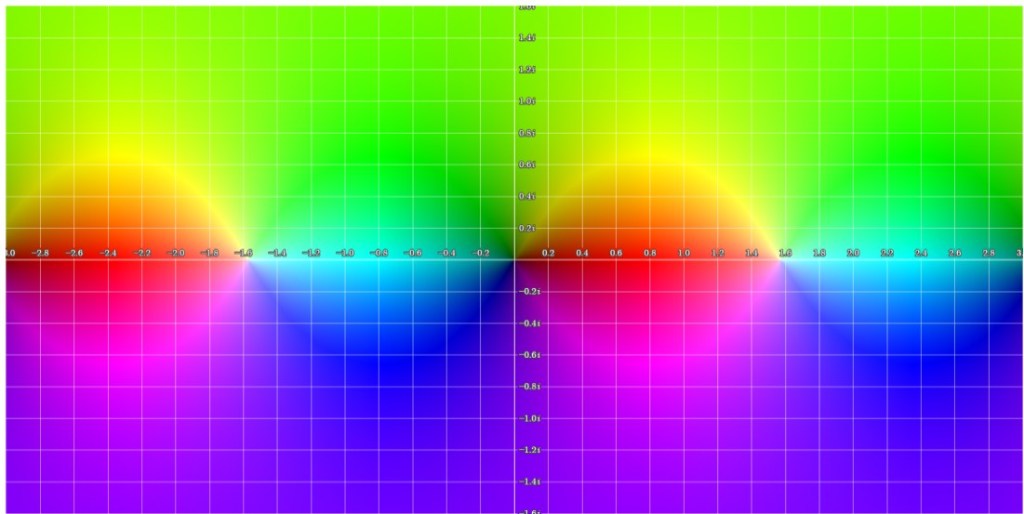
    We have observed (in particular through the examples concerning \tan(x) and \sec(x)) that Padé approximants:

    Converge beyond the disc of convergence of the entire series

    Speed up convergence

    Extend the notion of series

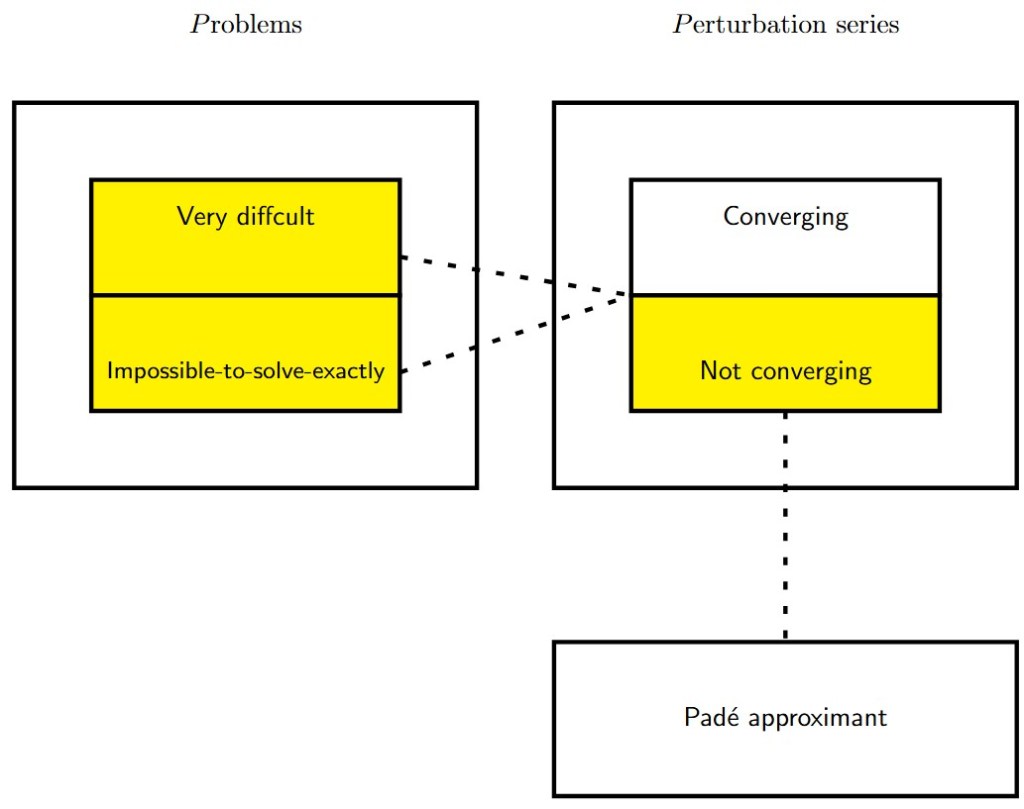
    Now, let’s imagine that we want to solve a problem that is very difficult or even impossible to solve exactly (i.e. a specific differential equation, extracting the roots of a polynomial, etc.). We can split the problem into an infinite number of simple problems. This is the principle of perturbation theory (which is in many cases the only way to solve the problem). The result of such a procedure is a geometric series (we will see this later). In a very large number of cases, this series does not converge. In these cases, we can use Padé approximants to ‘extract’ the information contained in the series and finally obtain a convergent rational function (as illustrated in the case of the functions \tan(x) and \sec(x)).

    The figure below presents schematically a potential application of Padé approximants in this context.

  • Padé approximants: Convergence examples

    We will first illustrate the Montessus’s theorem with the function:

    \displaystyle f(z) = \frac{z}{4 + z^2} = \frac{z}{(z - 2i)(z + 2i)}

    where z \in \mathbb{C}. This function has two poles at z = 2i and z = -2i.

    The corresponding Maclaurin series is:

    \displaystyle \frac{1}{4}z - \frac{1}{16}z^3 + \frac{1}{64}z^5 - \frac{1}{256}z^7 + \frac{1}{1024}z^9 + \mathcal{O}(z^{11})

    The corresponding P(2,2) approximant is (calculations were made according to the linear systems presented in this post):

    \displaystyle P(2,2) = \frac{z}{4 + z^2}

    We see that, in this case, if we set n = 2 (the total number of poles) we recover the original function since P(2,2) = f(z). The graphs of the f(z), P(2,2) and the corresponding Maclaurin series are presented in the figure below.

    Left, graph of

    \displaystyle \frac{z}{4 + z^2}

    and its corresponding P(2,2). Right, graph of the Maclaurin series

    \displaystyle \frac{1}{4}z - \frac{1}{16}z^3

    in the complex \mathbb{C}-plane. The poles at -2i and 2i are clearly visible on the left picture. Hue and brightness are used to display phase and magnitude, respectively.

    The Montessus’s theorem is also illustrated in the figures below for the function tan(z).

    \displaystyle P(2,2) = \frac{z}{1 - \frac{1}{3}z^2}

    and

    \displaystyle P(4,2) = \frac{z + \frac{1}{3}z^2}{1 - \frac{6}{15}z^2}

    of the \tan(z) function. The improvement of the approximation between P(2,2) and P(4,2) is visible on the figures.

    Graph of tan(z):

    Graphs of the P(2,2) (left) and P(4,2) (right) of tan(z):

    Pictures were produced using: Samuel Jinglian, 2018. “Complex Function Plotter.” https://samuelj.li/complex-function-plotter/.

  • Padé approximants: Convergence II

    In the previous post we gave a modern definition of Montessus’s theorem. Here is the original formulation from R. De Montessus (1902):

    “Il ressort de ces considérations qu’étant donnée une série de Taylor représentant une fonction f(x) dont les p pôles les plus rapprochés de l’origine sont intérieurs à un cercle (C) lui-même intérieur aux pôles suivants, chaque pôle multiple étant compté pour autant de pôles simples qu’il existe d’unités dans son degré de multiplicité, la fraction continue déduite de la ligne horizontale de rang p du Tableau de M. Padé, ce tableau étant composé de réduites normales, représente la fonction f(x) dans un cercle de rayon \displaystyle \lvert \alpha_{p+1} \lvert, où \alpha_{p+1} est l’affixe du pôle le plus rapproché de l’origine parmi tous ceux qui sont extérieurs au cercle (C). Si tous les pôles ont des modules différents, les fractions continues correspondant aux lignes horizontales représentent toute la fonction ; s’il existe simplement des discontinuités dans l’ensemble linéaire des modules des pôles, les fractions continues correspondant à des lignes horizontales convenablement choisies représentent encore la fonction. Si tous les pôles sont simples, la représentation a lieu dans des cercles d’autant plus grands que la ligne horizontale choisie est plus éloignée dans le Tableau. S’il y a des pôles multiples, il y a stationnement, en ce sens que plusieurs lignes horizontales consécutives représentant la fonction ont le même rayon de convergence. S’il y a enfin un point singulier essentiel, le stationnement se prolonge indéfiniment, aucune des fractions continues considérées ne représente la fonction en dehors du cercle sur la circonférence duquel se trouve le point singulier essentiel le plus rapproché de l’origine.”

    References:

    • R. De Montessus, “Sur les fractions continues algébriques”, Bulletin de la S. M. F., tome 30 (1902), p. 28-36.
    • E. B. Saff, “An extension of Montessus de Ballore’s theorem on the convergence of interpolating rational functions”, Journal of Approximation Theory, vol 6, No. 1, July 1972.

  • Padé approximants: Convergence I

    For row sequences on the Padé table, Montessus’s theorem (1902) proves convergence for functions meromorphic on a disk. Before giving the statement of the theorem, we would like to remind the reader of a few definitions:

    Holomorphic function: A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of each point in a given domain.

    Analytic function: An analytic function is a function that is locally given by a convergent power series.

    Meromorphic function: A meromorphic function on an open subset D of the complex \mathbb{C}-plane is a function that is holomorphic on all of D except for a set of isolated points. These points are called the ‘poles’ of the function.

    Here is the Montessus’s theorem as stated by E. B. Saff in 1972:

    Let f(z) be analytic at z = 0 and meromorphic with precisely \nu poles (multiplicity counted) in the disk |z| < \tau. Let D be the domain obtained from |z| < \tau by deleting the \nu poles of f(z). Then, for all m sufficiently large, there exists a unique rational function R_{m, \nu} of type (m, \nu), which interpolates f(z) in the point z = 0 considered of multiplicity m+\nu+1. Each R_{m, \nu} has precisely \nu finite poles and, as m \to \infty, these poles approach the \nu poles of f(z) in |z| < \tau. The sequence R_{m, \nu} converges in D to f(z), uniformly on any compact subset of D.

    Alternative formulation:

    Let f(z) be meromorphic in |z| < \tau, analytic at z = 0, and with a total of \nu poles \zeta_1, \zeta_2, \dots, \zeta_{\nu} (with multiplicity included) in |z| < \tau. Then, as m \to \infty, the Padé approximants P(m,\nu) of f converge on:

    \displaystyle S_f := \{ z \in \mathbb{C} \mid |z| < \tau \} \setminus \{ \zeta_1, \zeta_2, \dots, \zeta_\nu \}

    to f, uniformly on every compact subset K of S_f. In particular:

    \displaystyle P(m,\nu)(z) \to f(z)

    The Padé table is represented as follows:

    n=0 n=1 n=2 \dots n=\nu \dots
    m=0 P(0,0) P(0,1) P(0,2) \dots \boxed{P(0,\nu)} \dots
    m=1 P(1,0) P(1,1) P(1,2) \dots \boxed{P(1,\nu)} \dots
    m=2 P(2,0) P(2,1) P(2,2) \dots \boxed{P(2,\nu)} \dots
    \dots \dots \dots \dots \dots
    m \to \infty \dots \dots \dots \boxed{P(m,\nu)} \dots

    The Montessus’s theorem is crucial in approximation theory as it ensures the uniform convergence of Padé approximants for meromorphic functions, enhancing the accuracy of rational approximations.

  • Two properties of Padé Approximants

    Property 1

    Let g(x) = \frac{1}{f(x)}, with f(0) \neq 0, and assume f is at least C^{m+n} at x = 0. If P(m,n)_f = \frac{P(x)}{Q(x)}, then the [n/m] Padé approximant of g(x):

    \displaystyle P(n,m)_g = \frac{Q(x)}{P(x)},

    provided P(0) \neq 0.

    Proof: Given P(m,n)_f = \frac{P(x)}{Q(x)}, we have:

    \displaystyle f(x) Q(x) - P(x) = \epsilon(x) x^{m+n+1}.

    Since g(x) = \frac{1}{f(x)}, consider:

    \displaystyle g(x) P(x) - Q(x) = \frac{1}{f(x)} P(x) - Q(x) = \frac{P(x) - f(x) Q(x)}{f(x)} = -\frac{\epsilon(x) x^{m+n+1}}{f(x)}.

    Since f(0) \neq 0, \frac{1}{f(x)} is bounded near x = 0, and:

    \displaystyle g(x) P(x) - Q(x) = O(x^{m+n+1}),

    indicating that \frac{Q(x)}{P(x)} is the [n/m] Padé approximant of g(x), as it matches the Taylor series of g(x) up to x^{m+n}. For example, for f(x) = \sqrt{1+x}, the [2/2] Padé approximant can be computed, and g(x) = \frac{1}{\sqrt{1+x}} yields a consistent [2/2] approximant by taking the reciprocal.

    Property 2

    If f is even (f(x) = f(-x)) and at least C^{m+n}, and the [m/n] Padé approximant exists and is unique (guaranteed if the Hankel determinant is non-zero), then P(m,n)_f = \frac{P(x)}{Q(x)} is even, i.e., P(x) = P(-x) and Q(x) = Q(-x).

    Proof: Since f(x) = f(-x), the Taylor series of f contains only even powers. For P(m,n)_f = \frac{P(x)}{Q(x)}, we have:

    \displaystyle f(x) Q(x) - P(x) = O(x^{m+n+1}).

    Evaluate at -x:

    \displaystyle f(-x) Q(-x) - P(-x) = f(x) Q(-x) - P(-x) = O(x^{m+n+1}),

    since f(-x) = f(x), and the error term remains of order x^{m+n+1}. Thus, \frac{P(-x)}{Q(-x)} satisfies the same Padé condition as \frac{P(x)}{Q(x)}. By uniqueness of the [m/n] approximant (assuming non-zero Hankel determinant), we conclude:

    \displaystyle P(x) = P(-x), \quad Q(x) = Q(-x).

  • Padé approximant of 1/(1-x)

    In this post we will have a look at the Padé approximants of \frac{1}{1-x}. The Maclaurin series of \frac{1}{1-x} is:

    \displaystyle 1 + x + x^2 + x^3 + x^4 + x^5 + \cdots

    which converges for x \in ]-1,1[. We can calculate the corresponding P(1,1)

    \displaystyle \frac{A_0 + A_1 x}{1 + B_1 x} = 1 + x + x^2 + \cdots
    \displaystyle = (1 + B_1 x)(1 + x + x^2 + \cdots)
    \displaystyle = 1 + x + x^2 + \cdots + B_1 x + B_1 x^2 + B_1 x^3 + \cdots
    \displaystyle = 1 + (1 + B_1) x + (1 + B_1) x^2 + (1 + B_1) x^3 + \cdots

    Keeping only degrees up to 2:

    \displaystyle = 1 + (1 + B_1) x + (1 + B_1) x^2

    This implies:

    \displaystyle A_0 = 1
    \displaystyle A_1 = 1 + B_1
    \displaystyle 1 + B_1 = 0

    Therefore, A_0 = 1, A_1 = 0 and B_1 = -1 and the P(1,1) is:

    \displaystyle \boxed{P(1,1)(x) = \frac{1}{1-x}}

    This is an exceptional result since the Padé approximant P(1,1) is equal to the function it is supposed to approximate. This result is very attractive since it suggests a way to solve very hard problems using series up to some terms. Then using Padé approximation we may hope to recover the exact solution (or at least a sufficient approximation for a specific application).

    Let’s imagine that we would like to solve the following differential equation:

    \displaystyle y' = y^2 \text{ with initial condition } y(0) = 1

    This differential equation can be solved exactly since it is separable. The solution is y(x) = \frac{1}{1-x}. Let’s pretend for a moment that solving this equation is a very difficult problem because we don’t know how to solve separable differential equations.

    A possible approach is to consider a solution of the form:

    \displaystyle y(x) = a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \cdots

    Then we have:

    \displaystyle y(x)' = a_1 + 2 a_2 x + 3 a_3 x^2 + \cdots
    \displaystyle y(x)^2 = (a_0 + a_1 x + a_2 x^2 + \cdots)^2
    \displaystyle = a_0^2 + a_0 a_1 x + a_0 a_2 x^2 + \cdots
    \displaystyle + a_0 a_1 x + a_1^2 x^2 + \cdots
    \displaystyle + a_2 a_0 x^2 + \cdots
    \displaystyle = a_0^2 + 2 a_0 a_1 x + (a_1^2 + 2 a_0 a_2) x^2 + \cdots

    We can write the differential equation keeping only terms up to two:

    \displaystyle y(x)' = y(x)^2
    \displaystyle a_1 + 2 a_2 x + 3 a_3 x^2 = a_0^2 + 2 a_0 a_1 x + (a_1^2 + 2 a_0 a_2) x^2

    we obtain:

    \displaystyle a_1 = a_0^2
    \displaystyle 2 a_2 = 2 a_0 a_1
    \displaystyle 3 a_3 = a_1^2 + 2 a_0 a_2

    Setting a_0 = 1 (since y(0) = 1) implies a_1 = a_2 = a_3 = 1. An approximation of the solution to the differential equation is therefore:

    \displaystyle 1 + x + x^2 + x^3

    As presented above, the corresponding P(1,1) = \frac{1}{1-x} which is the exact solution to the differential equation. In fact, the diagonal sequence of Padé approximants (P(1,1), P(2,2), … P(n,n)) recovers \frac{1}{1-x}. This is, of course, a special case.

    So, for this differential equation, we have the following pattern:

  • Padé approximants of sqrt(1+x) and 1/sqrt(1+x)

    In this post we will have a look at the Padé approximants of \sqrt{1+x} and \frac{1}{\sqrt{1+x}}. The Maclaurin series of \sqrt{1+x} is:

    \displaystyle 1+ \frac{1}{2}x - \frac{1}{8} x^2 + \frac{1}{16}x^3 - \frac{5}{128} x^4 + \frac{7}{256}x^5 + \dots

    The MacLaurin series of \frac{1}{\sqrt{1+x}} is:

    \displaystyle 1 - \frac{1}{2}x + \frac{3}{8}x^2 - \frac{5}{16}x^3 + \frac{35}{128}x^4 + \dots

    According to the section concerning the calculation of Padé approximants using a matrix notation (see post Computing Padé approximants, we have to solve two linear systems sequentially. For \sqrt{1+x} we therefore have to first solve:

    \displaystyle \begin{pmatrix} C_1 & C_2 \\ C_2 & C_3 \end{pmatrix} \begin{pmatrix} B_2 \\ B_1 \end{pmatrix} = -\begin{pmatrix} C_3 \\ C_4 \end{pmatrix}
    \displaystyle \begin{pmatrix} \frac{1}{2} & -\frac{1}{8} \\ -\frac{1}{8} & \frac{1}{16} \end{pmatrix} \begin{pmatrix} B_2 \\ B_1 \end{pmatrix} = \begin{pmatrix} -\frac{1}{16} \\ \frac{5}{128} \end{pmatrix}
    \displaystyle \begin{pmatrix} B_2 \\ B_1 \end{pmatrix} = \begin{pmatrix} \frac{1}{2} & -\frac{1}{8} \\ -\frac{1}{8} & \frac{1}{16} \end{pmatrix}^{-1} \begin{pmatrix} -\frac{1}{16} \\ \frac{5}{128} \end{pmatrix}
    \displaystyle \begin{pmatrix} B_2 \\ B_1 \end{pmatrix} = \begin{pmatrix} 4 & 8 \\ 8 & 32 \end{pmatrix} \begin{pmatrix} -\frac{1}{16} \\ \frac{5}{128} \end{pmatrix}
    \displaystyle \begin{pmatrix} B_2 \\ B_1 \end{pmatrix} = \begin{pmatrix} \frac{1}{16} \\ \frac{3}{4} \end{pmatrix}

    Injecting the B_n coefficients calculated above in the second linear system we have:

    \displaystyle \begin{pmatrix} C_0 & 0 & 0 \\ C_1 & C_0 & 0 \\ C_2 & C_1 & C_0 \end{pmatrix} \begin{pmatrix} B_0 \\ B_1 \\ B_2 \end{pmatrix} = \begin{pmatrix} A_0 \\ A_1 \\ A_2 \end{pmatrix}
    \displaystyle \begin{pmatrix} 1 & 0 & 0 \\ \frac{1}{2} & 1 & 0 \\ -\frac{1}{8} & \frac{1}{2} & 1 \end{pmatrix} \begin{pmatrix} 1 \\ \frac{3}{4} \\ \frac{1}{16} \end{pmatrix} = \begin{pmatrix} A_0 \\ A_1 \\ A_2 \end{pmatrix}

    From this system we obtain A_0 = 1, A_1 = \frac{5}{4}, A_2 = \frac{5}{16}. Therefore:

    \displaystyle P(2,2) = \frac{A_0 + A_1 x + A_2 x^2}{1 + B_1 x + B_2 x^2}
    \displaystyle = \frac{1 +\frac{5}{4} x + \frac{5}{16} x^2}{1 + \frac{3}{4} x + \frac{1}{16} x^2}

    For \frac{1}{\sqrt{1+x}} we have to first solve:

    \displaystyle \begin{pmatrix} C_1 & C_2 \\ C_2 & C_3 \end{pmatrix} \begin{pmatrix} B_2 \\ B_1 \end{pmatrix} = -\begin{pmatrix} C_3 \\ C_4 \end{pmatrix}
    \displaystyle \begin{pmatrix} -\frac{1}{2} & \frac{3}{8} \\ \frac{3}{8} & -\frac{5}{16} \end{pmatrix} \begin{pmatrix} B_2 \\ B_1 \end{pmatrix} = \begin{pmatrix} \frac{5}{16} \\ -\frac{35}{128} \end{pmatrix}
    \displaystyle \begin{pmatrix} B_2 \\ B_1 \end{pmatrix} = \begin{pmatrix} -\frac{1}{2} & \frac{3}{8} \\ \frac{3}{8} & -\frac{5}{16} \end{pmatrix}^{-1} \begin{pmatrix} \frac{5}{16} \\ -\frac{35}{128} \end{pmatrix}
    \displaystyle \begin{pmatrix} B_2 \\ B_1 \end{pmatrix} = \begin{pmatrix} -20 & -24 \\ -24 & -32 \end{pmatrix} \begin{pmatrix} \frac{5}{16} \\ -\frac{35}{128} \end{pmatrix}
    \displaystyle \begin{pmatrix} B_2 \\ B_1 \end{pmatrix} = \begin{pmatrix} \frac{5}{16} \\ \frac{5}{4} \end{pmatrix}

    Injecting the B_n coefficients calculated above in the second linear system we have:

    \displaystyle \begin{pmatrix} C_0 & 0 & 0 \\ C_1 & C_0 & 0 \\ C_2 & C_1 & C_0 \end{pmatrix} \begin{pmatrix} B_0 \\ B_1 \\ B_2 \end{pmatrix} = \begin{pmatrix} A_0 \\ A_1 \\ A_2 \end{pmatrix}
    \displaystyle \begin{pmatrix} 1 & 0 & 0 \\ -\frac{1}{2} & 1 & 0 \\ \frac{3}{8} & -\frac{1}{2} & 1 \end{pmatrix} \begin{pmatrix} 1 \\ \frac{5}{4} \\ \frac{5}{16} \end{pmatrix} = \begin{pmatrix} A_0 \\ A_1 \\ A_2 \end{pmatrix}

    From this system we obtain A_0 = 1, A_1 = \frac{3}{4}, A_2 = \frac{1}{16}. Therefore:

    \displaystyle P(2,2) = \frac{A_0 + A_1 x + A_2 x^2}{1 + B_1 x + B_2 x^2}
    \displaystyle = \frac{1 + \frac{3}{4} x + \frac{1}{16} x^2}{1 + \frac{5}{4} x + \frac{5}{16} x^2}

    We observe that:

    \displaystyle P(2,2)_{\frac{1}{\sqrt{1+x}}} = \frac{1}{P(2,2)_{\sqrt{1+x}}}

    These calculations suggest that, if g = \frac{1}{f} then:

    P(n,m)_{g} = \frac{1}{P(n,m)_{f}}

    Where P(n,m)_{g} and P(n,m)_{f} are the Padé approximants of g and f respectively. This proposition is actually true and can be proved formally.

  • Padé approximants of sec(x)

    In the previous post we have computed the Padé approximants for the exp(x) function. The approximation was not very impressive compared to the Maclaurin series of exp() since the latter converges for all x. In this post we will have a look at the Padé approximants and Maclaurin series of sec(x).

    First let’s recall the graph of sec(x) (see figure 1). sec(x) is a function with vertical asymptotes that cannot be approximated globally by a Taylor series. The Maclaurin series of sec(x) is:

    \displaystyle sec(x) = 1 + \frac{1}{2!}x^2 + \frac{5}{4!} x^4 + \frac{61}{6!} x^6 + \frac{1385}{8!} x^8 + \cdots
    \displaystyle = \sum_{n=0}^{\infty} \frac{E_n}{(2n)!} x^{2n}

    Where E_n are so-called Euler numbers:

    \displaystyle E_1 = 1, \quad E_2 = 5, \quad E_3 = 61, \quad E_4 = 1385, \quad E_5 = 50521, \quad E_6 = 2702765

    We would like to compute the P(4,4) approximant of sec(x). The first step is to have a look at the corresponding Hankel determinant (which is the determinant of the Hankel matrix):

    \displaystyle H_{n,m}(f) = \det \left( \begin{array}{cccc} C_{m-n+1} & C_{m-n+2} & \cdots & C_m \\ C_{m-n+2} & C_{m-n+3} & \cdots & C_{m+1} \\ \vdots & \vdots & \ddots & \vdots \\ C_m & C_{m+1} & \cdots & C_{m+n-1} \end{array} \right)

    For m = 4 and n = 4 we have:

    \displaystyle H_{4,4}(f) = \det \left( \begin{array}{cccc} C_1 & C_2 & C_3 & C_4 \\ C_2 & C_3 & C_4 & C_5 \\ C_3 & C_4 & C_5 & C_6 \\ C_4 & C_5 & C_6 & C_7 \end{array} \right)

    and the corresponding Hankel determinant for the P(4,4) of sec(x) is:

    \displaystyle H_{4,4}(sec(x)) = \det \left( \begin{array}{cccc} 0 & \frac{1}{2!} & 0 & \frac{5}{4!} \\ \frac{1}{2!} & 0 & \frac{5}{4!} & 0 \\ 0 & \frac{5}{4!} & 0 & \frac{61}{6!} \\ \frac{5}{4!} & 0 & \frac{61}{6!} & 0 \end{array} \right) = 1.08507 \times 10^{-6}

    the determinant being not equal to zero implies that we can inverse the Hankel matrix and solve the systems to compute the Padé coefficients of P(4,4) for sec(x) (see post Computing Padé approximants). The inverse of the Hankel matrix is given by:

    \displaystyle \left( \begin{array}{cccc} 0 & -81.3333 & 0 & 200 \\ -81.3333 & 0 & 200 & 0 \\ 0 & 200 & 0 & -480 \\ 200 & 0 & -480 & 0 \end{array} \right)

    We have to solve this first linear system:

    \displaystyle \left( \begin{array}{cccc} 0 & \frac{1}{2!} & 0 & \frac{5}{4!} \\ \frac{1}{2!} & 0 & \frac{5}{4!} & 0 \\ 0 & \frac{5}{4!} & 0 & \frac{61}{6!} \\ \frac{5}{4!} & 0 & \frac{61}{6!} & 0 \end{array} \right) \left( \begin{array}{c} B_4 \\ B_3 \\ B_2 \\ B_1 \end{array} \right) = - \left( \begin{array}{c} C_5 \\ C_6 \\ C_7 \\ C_8 \end{array} \right) = \left( \begin{array}{c} 0 \\ -\frac{61}{6!} \\ 0 \\ -\frac{1385}{8!} \end{array} \right)
    \displaystyle \left( \begin{array}{cccc} 0 & \frac{1}{2!} & 0 & \frac{5}{4!} \\ \frac{1}{2!} & 0 & \frac{5}{4!} & 0 \\ 0 & \frac{5}{4!} & 0 & \frac{61}{6!} \\ \frac{5}{4!} & 0 & \frac{61}{6!} & 0 \end{array} \right)^{-1} \left( \begin{array}{c} 0 \\ -\frac{61}{6!} \\ 0 \\ -\frac{1385}{8!} \end{array} \right) = \left( \begin{array}{c} B_4 \\ B_3 \\ B_2 \\ B_1 \end{array} \right)
    \displaystyle \left( \begin{array}{cccc} 0 & -81.3333 & 0 & 200 \\ -81.3333 & 0 & 200 & 0 \\ 0 & 200 & 0 & -480 \\ 200 & 0 & -480 & 0 \end{array} \right) \left( \begin{array}{c} 0 \\ -\frac{61}{6!} \\ 0 \\ -\frac{1385}{8!} \end{array} \right) = \left( \begin{array}{c} \frac{104.3191}{5040} \\ 0 \\ -\frac{115}{252} \\ 0 \end{array} \right)

    Solving the system above allows us to compute the B_n coefficients (see results below). Now, according to the calculations presented in the post (see Computing Padé approximants), we have to solve the second linear system to compute the A_m coefficients:

    \displaystyle \left( \begin{array}{ccccc} C_0 & 0 & 0 & 0 & 0 \\ C_1 & C_0 & 0 & 0 & 0 \\ C_2 & C_1 & C_0 & 0 & 0 \\ C_3 & C_2 & C_1 & C_0 & 0 \\ C_4 & C_3 & C_2 & C_1 & C_0 \end{array} \right) \left( \begin{array}{c} 1 \\ B_1 \\ B_2 \\ B_3 \\ B_4 \end{array} \right) = \left( \begin{array}{c} A_0 \\ A_1 \\ A_2 \\ A_3 \\ A_4 \end{array} \right)
    \displaystyle \left( \begin{array}{ccccc} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ \frac{1}{2!} & 0 & 1 & 0 & 0 \\ 0 & \frac{1}{2!} & 0 & 1 & 0 \\ \frac{5}{4!} & 0 & \frac{1}{2!} & 0 & 1 \end{array} \right) \left( \begin{array}{c} 1 \\ 0 \\ -\frac{115}{252} \\ 0 \\ \frac{104.3191}{5040} \end{array} \right) = \left( \begin{array}{c} A_0 \\ A_1 \\ A_2 \\ A_3 \\ A_4 \end{array} \right)
    \displaystyle A_0 = 1, \quad A_1 = 0, \quad A_2 = \frac{1}{2!} - \frac{115}{252} = \frac{11}{252}, \quad A_3 = 0, \quad A_4 = \frac{5}{24} - \frac{115}{504} + \frac{104.3191}{5040} = \frac{4.3191}{5040}
    \displaystyle B_0 = 1, \quad B_1 = 0, \quad B_2 = -\frac{115}{252}, \quad B_3 = 0, \quad B_4 = \frac{104.3191}{5040}

    This implies that for sec(x):

    \displaystyle P(4,4) = \frac{1 + A_2 x^2 + A_4 x^4}{1 + B_2 x^2 + B_4 x^4}
    \displaystyle = \frac{1 + \frac{11}{252} x^2 + \frac{4.3191}{5040} x^4}{1 - \frac{115}{252} x^2 + \frac{104.3191}{5040} x^4}

    The graph of P(4,4) for sec(x) is presented in figure 2. The graph of sec(x) and its corresponding P(4,4) is presented in figure 3. We can see that the P(4,4) approximant (in green) is approximating the function sec(x) beyond its vertical asymptotes (pink vertical lines) in contrast to the corresponding Taylor series presented in figure 1. Moreover the convergence of P(4,4) is better than the one of the Taylor series.

    It is also interesting to note that the ‘information’ needed to construct the Padé approximants of the function sec(x) has been extracted from the truncated Taylor series. Despite this fact, the Padé approximant provides a better approximation of the sec(x) function than the series from which it is derived.

  • Padé approximants of exp(x)

    We can organize and present the Padé  P(m,n)  approximants in a table like this:

     P(m,n)   0   1   2   3   ... 
     0   P(0,0)   P(1,0)   P(2,0)   P(3,0)   ... 
     1   P(0,1)   P(1,1)   P(2,1)   P(3,1)   ... 
     2   P(0,2)   P(1,2)   P(2,2)   P(3,2)   ... 
     3   P(0,3)   P(1,3)   P(2,3)   P(3,3)   ... 
     ...   ...   ...   ...   ...   ... 

    The table above shows, in order, Padé’s first approximants. This is a way to present and organize the Padé approximants. We can use the procedure presented in the previous posts to compute the Padé approximants for the exponential function  \exp(x) . Solving systems presented in the previous posts, leads to the following table:

     P(m,n)   0   1   2   3   ... 
     0   1   1 + x   1 + x + \frac{x^2}{2}   1 + x + \frac{x^2}{2} + \frac{x^3}{6}   ... 
     1   \frac{1}{1 - x}   \frac{1 + \frac{1}{2}x}{1 - \frac{1}{2}x}   \frac{1 + \frac{2}{3}x + \frac{1}{6}x^2}{1 - \frac{1}{3}x}   \frac{1 + \frac{3}{4}x + \frac{1}{4}x^2 + \frac{1}{24}x^3}{1 - \frac{1}{4}x}   ... 
     2   \frac{1}{1 - x + \frac{1}{2}x^2}   \frac{1 + \frac{1}{3}x}{1 - \frac{2}{3}x + \frac{1}{6}x^2}   \frac{1 + \frac{1}{2}x + \frac{1}{12}x^2}{1 - \frac{1}{2}x + \frac{1}{12}x^2}   \frac{1 + \frac{3}{5}x + \frac{3}{20}x^2 + \frac{1}{60}x^3}{1 - \frac{2}{5}x + \frac{1}{20}x^2}   ... 
     3   \frac{1}{1 - x + \frac{1}{2}x^2 - \frac{1}{6}x^3}   \frac{1 + \frac{1}{4}x}{1 - \frac{3}{4}x + \frac{1}{4}x^2 - \frac{1}{24}x^3}   \frac{1 + \frac{2}{5}x + \frac{1}{20}x^2}{1 - \frac{3}{5}x + \frac{3}{20}x^2 - \frac{1}{60}x^3}   \frac{1 + \frac{1}{2}x + \frac{1}{10}x^2 + \frac{1}{120}x^3}{1 - \frac{1}{2}x + \frac{1}{10}x^2 - \frac{1}{120}x^3}   ... 
     ...   ...   ...   ...   ...   ... 

    Setting x = 1, we obtain the following values:

     P(m,n)   0   1   2   3 
     0   1.000000   2.000000   2.500000   2.666667 
     1  —  3.000000   2.750000   2.722222 
     2   2.000000   2.666667   2.714286   2.717949 
     3   3.000000   2.727273   2.718750   2.718310 

    The ‘relative error’ is defined as:

    \displaystyle \text{Relative error} := \frac{\text{Approximation} - \text{Exact value}}{\text{Exact value}}

    Relative errors of Padé approximants  P(m,n)  of  e^x  evaluated at x = 1, using the exact value  e \approx 2.718281  are shown in the table below:

     P(m,n)   0   1   2   3 
     0   -0.632121   -0.264241   -0.080301   -0.018988 
     1  —  0.103638   0.011662   0.001449 
     2   -0.264241   -0.018988   -0.001471   -0.000122 
     3   0.103638   0.003307   0.000172   0.000010 

    The Padé approximants exhibit an alternating sign pattern in their relative errors. This indicates that the Padé approximants oscillate around the true value  e , approaching it from both sides. In contrast, the Taylor approximations converge monotonically from below.

  • Hankel determinant

    In the previous posts, we have seen that in order to compute the Padé coefficients P(m,n) corresponding to a given geometric series we have to be invert the following matrix:

    \displaystyle \begin{pmatrix} C_{m-n+1} & C_{m-n+2} & \ldots & C_{m} \\ C_{m-n+2} & C_{m-n+3} & \ldots & C_{m+1} \\ \vdots & & & \vdots \\ C_{m} & C_{m+1} & \ldots & C_{m+n-1} \end{pmatrix}

    Where C_l are the coefficients of the Taylor series. The matrix above is called a “Hankel matrix”. A ‘Hankel Matrix’ is a symmetric square matrix in which each ascending skew-diagonal from left to right is constant. For Example a Hankel matrix of size 5 can be written like this:

    \displaystyle \begin{pmatrix} a & b & c & d & e \\ b & c & d & e & f \\ c & d & e & f & g \\ d & e & f & g & h \\ e & f & g & h & i \end{pmatrix}

    Let’s make some observations on the Hankel determinant H_{n,m}(f):

    \displaystyle H_{n,m}(f) := \begin{vmatrix} C_{m-n+1} & C_{m-n+2} & \ldots & C_{m} \\ C_{m-n+2} & C_{m-n+3} & \ldots & C_{m+1} \\ \vdots & & & \vdots \\ C_{m} & C_{m+1} & \ldots & C_{m+n-1} \end{vmatrix}

    This determinant has n colons and n rows. We can also numerate the terms of the determinant following the notation:

    \displaystyle H_{n,m}(f) := \begin{vmatrix} d(1,1) & d(1,2) & \ldots & d(1,n) \\ d(2,1) & d(2,2) & \ldots & d(2,n) \\ \vdots & & & \vdots \\ d(n,1) & d(n,2) & \ldots & d(n,n) \end{vmatrix}

    Where d(1,1) := C_{m-n+1} etc. This notation of the terms of the determinants implies that:

    \displaystyle d(i,j) = C_{m-n+i+j-1}

    So that:

    \displaystyle d(1,1) = C_{m-n+1+1-1} = C_{m-n+1}
    \displaystyle d(1,2) = C_{m-n+1+2-1} = C_{m-n+2}
    \displaystyle d(2,1) = C_{m-n+2+1-1} = C_{m-n+2}
    \displaystyle \ldots
    \displaystyle d(n,n) = C_{m-n+n+n-1} = C_{m+n-1}

    If f(x) is a even function of class C_{\infty}, we see that odd coefficients C_{2p+1} = \frac{f^{(2p+1)}(0)}{(2p+1)!} = 0. In this case, every second term of in the Hankel matrix is zero. If f(x) is even, we can establish that if m and n are odd then the Hankel determinant is zero:

    The term with index d(i,j) of the Hankel determinant is C_{m-n+i+j-1}. As stated before, this term is zero for an even function if m-n+i+j-1 is odd. Now, if m and n are odd this means that n-m is even and m-n+i+j-1 is odd when i + j is even. It follows that, in the case of an even function, the Hankel determinant is of the form:

    \displaystyle \begin{vmatrix} 0 & b & 0 & d & \hdots \\ b & 0 & d & 0 & \hdots \\ 0 & d & 0 & f & \hdots \\ \vdots & \vdots & \vdots & & \ddots \end{vmatrix}

    We observe that the odd rows of this determinant are linear combinations of:

    \displaystyle \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ \vdots \end{pmatrix}, \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ \vdots \end{pmatrix} \text{, etc.}

    This implies that odd-numbered columns are linked and therefore the determinant is zero.

    As example we will derive the P(3,3) of the cosine function. First we have to consider the geometric series of degrees up to 3 + 3 = 6 of cosine:

    \displaystyle \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \mathcal{O}(x^8)

    For m=3 and n=3 (m and n are both odd) the Hankel determinant is:

    \displaystyle H_{3,3}(f) = \begin{vmatrix} C_{1} & C_{2} & C_{3} \\ C_{2} & C_{3} & C_{4} \\ C_{3} & C_{4} & C_{5} \end{vmatrix}

    The corresponding Hankel determinant for calculating the coefficients of the P(3,3) Padé approximant of the geometric series of cosine is therefore:

    \displaystyle H_{3,3}(cos) = \begin{vmatrix} 0 & -\frac{1}{2} & 0 \\ -\frac{1}{2} & 0 & \frac{1}{4!} \\ 0 & \frac{1}{4!} & 0 \end{vmatrix} = 0

    This implies that we cannot calculate the P(3,3) approximant for the cosine function.

    In conclusion, for an even function like cosine, when m and n are odd, the Hankel determinant Hn,m(f) is zero due to the linear dependence of the columns.