Approximaths

Zeta summation II

Written by

approximaths

in

Now look at:

\displaystyle f(z) = e^{-\pi z^2}

where z \in \mathbb{C}. This function is an entire function (differentiable in the entire complex plane). Since this function is entire the Cauchy’s integral theorem applies:

\displaystyle \int_{\gamma_1} f(z)\,dz = 0

Where \gamma_1 is any closed contour in the complex plane. Let us consider the contour presented in the figure below:

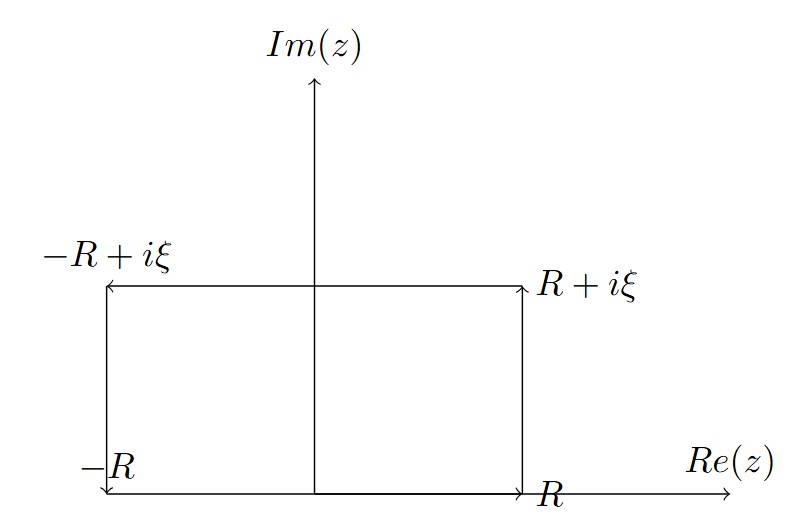
\displaystyle \int_{-R}^{R} f(z) \,dz + \int_{R}^{R+ i \xi} f(z) \,dz + \int_{R+ i \xi}^{-R+ i \xi} f(z) \,dz + \int_{-R+ i \xi}^{-R} f(z) \,dz = 0

For the first term of the integral we set: z(t) = t.
For the second term: z(t) = R + it.
For the third term: z(t) = t + i \xi.
For the fourth term: z(t) = -R + it.
The integral becomes:

\displaystyle \int_{-R}^{R} f(t) \,dt + \int_{R}^{R+ i \xi} f(R + it) i\,dt + \int_{R+ i \xi}^{-R+ i \xi} f(t + i \xi) \,dt + \int_{-R+ i \xi}^{-R} f(-R + it) i\,dt =
\displaystyle \int_{-R}^{R} f(t) \,dt + \int_{0}^{\xi} f(R + it) i\,dt + \int_{R}^{-R} f(t + i \xi) \,dt + \int_{\xi}^{0} f(-R + it) i\,dt =
\displaystyle \int_{-R}^{R} e^{-\pi t^2} \,dt + \int_{0}^{\xi} e^{-\pi (R + it)^2} i\,dt + \int_{R}^{-R} e^{-\pi (t + i \xi)^2} \,dt + \int_{\xi}^{0} e^{-\pi (-R + it)^2} i\,dt = 0

Observe that the last term is equal to (using u = -t):

\displaystyle \int_{\xi}^{0} e^{-\pi (-R + it)^2} i\,dt = -\int_{-\xi}^{0} e^{-\pi (-R - iu)^2} i\,du

The term (-R - iu)^2 can be written (R + iu)^2:

\displaystyle \int_{\xi}^{0} e^{-\pi (-R + it)^2} i\,dt = -\int_{-\xi}^{0} e^{-\pi (R + iu)^2} i\,du

now:

\displaystyle -\int_{-\xi}^{0} e^{-\pi (R + iu)^2} i\,du = - \left( -\int_{0}^{-\xi} e^{-\pi (R + iu)^2} i\,du \right) = \int_{0}^{-\xi} e^{-\pi (R + iu)^2} i\,du

The second and fourth term cancel and the equation above becomes:

\displaystyle \int_{-R}^{R} e^{-\pi t^2} dt + \int_{R}^{-R} e^{-\pi (t + i \xi)^2}\,dt = 0 \\ \int_{-R}^{R} e^{-\pi t^2} dt = - \int_{R}^{-R} e^{-\pi (t + i \xi)^2}\,dt \\ \int_{-R}^{R} e^{-\pi t^2} dt = \int_{-R}^{R} e^{-\pi (t^2 + 2 t i \xi - \xi^2)}\,dt \\ \int_{-R}^{R} e^{-\pi t^2} dt = e^{\pi \xi^2} \int_{-R}^{R} e^{-\pi t^2} e^{-2\pi i t \xi}\,dt \\

Using

\displaystyle \lim_{R \to \infty} \int_{-R}^{R} e^{-\pi t^2}\,dt = 1

Therefore, if \xi \in \mathbb{R}:

\displaystyle e^{-\pi \xi^2} = \int_{-\infty}^{\infty} e^{-\pi x^2} e^{-2\pi i x \xi} \,dx

We conclude from this post and the previous post that the Gaussian function e^{-\pi \xi^2} is its own Fourier transform.

Comments

Leave a comment

More posts