Month: December 2025

Zeta summation II

Now look at:

$\displaystyle f(z) = e^{-\pi z^2}$

where $z \in \mathbb{C}$ . This function is an entire function (differentiable in the entire complex plane). Since this function is entire the Cauchy’s integral theorem applies:

$\displaystyle \int_{\gamma_1} f(z)\,dz = 0$

Where $\gamma_1$ is any closed contour in the complex plane. Let us consider the contour presented in the figure below:

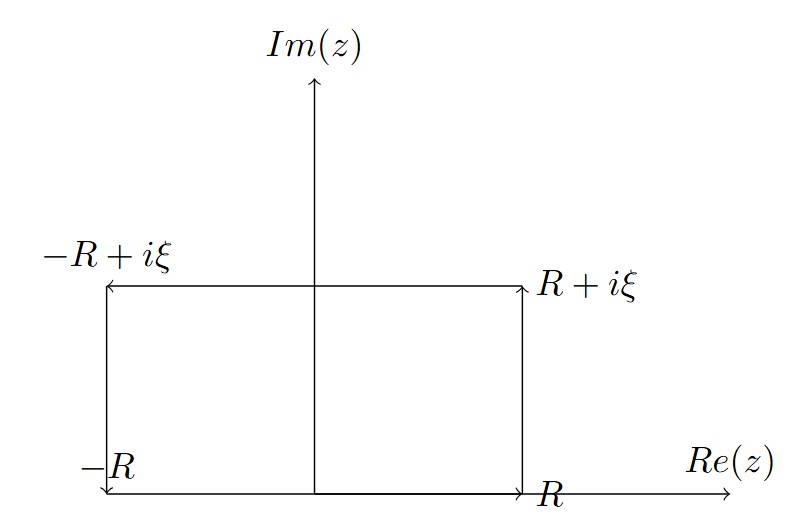
$\displaystyle \int_{-R}^{R} f(z) \,dz + \int_{R}^{R+ i \xi} f(z) \,dz + \int_{R+ i \xi}^{-R+ i \xi} f(z) \,dz + \int_{-R+ i \xi}^{-R} f(z) \,dz = 0$

For the first term of the integral we set: $z(t) = t$ .
For the second term: $z(t) = R + it$ .
For the third term: $z(t) = t + i \xi$ .
For the fourth term: $z(t) = -R + it$ .
The integral becomes:

$\displaystyle \int_{-R}^{R} f(t) \,dt + \int_{R}^{R+ i \xi} f(R + it) i\,dt + \int_{R+ i \xi}^{-R+ i \xi} f(t + i \xi) \,dt + \int_{-R+ i \xi}^{-R} f(-R + it) i\,dt =$

$\displaystyle \int_{-R}^{R} f(t) \,dt + \int_{0}^{\xi} f(R + it) i\,dt + \int_{R}^{-R} f(t + i \xi) \,dt + \int_{\xi}^{0} f(-R + it) i\,dt =$

$\displaystyle \int_{-R}^{R} e^{-\pi t^2} \,dt + \int_{0}^{\xi} e^{-\pi (R + it)^2} i\,dt + \int_{R}^{-R} e^{-\pi (t + i \xi)^2} \,dt + \int_{\xi}^{0} e^{-\pi (-R + it)^2} i\,dt = 0$

Observe that the last term is equal to (using u = -t):

$\displaystyle \int_{\xi}^{0} e^{-\pi (-R + it)^2} i\,dt = -\int_{-\xi}^{0} e^{-\pi (-R - iu)^2} i\,du$

The term $(-R - iu)^2$ can be written $(R + iu)^2$ :

$\displaystyle \int_{\xi}^{0} e^{-\pi (-R + it)^2} i\,dt = -\int_{-\xi}^{0} e^{-\pi (R + iu)^2} i\,du$

now:

$\displaystyle -\int_{-\xi}^{0} e^{-\pi (R + iu)^2} i\,du = - \left( -\int_{0}^{-\xi} e^{-\pi (R + iu)^2} i\,du \right) = \int_{0}^{-\xi} e^{-\pi (R + iu)^2} i\,du$

The second and fourth term cancel and the equation above becomes:

$\displaystyle \int_{-R}^{R} e^{-\pi t^2} dt + \int_{R}^{-R} e^{-\pi (t + i \xi)^2}\,dt = 0 \\ \int_{-R}^{R} e^{-\pi t^2} dt = - \int_{R}^{-R} e^{-\pi (t + i \xi)^2}\,dt \\ \int_{-R}^{R} e^{-\pi t^2} dt = \int_{-R}^{R} e^{-\pi (t^2 + 2 t i \xi - \xi^2)}\,dt \\ \int_{-R}^{R} e^{-\pi t^2} dt = e^{\pi \xi^2} \int_{-R}^{R} e^{-\pi t^2} e^{-2\pi i t \xi}\,dt \\$

Using

$\displaystyle \lim_{R \to \infty} \int_{-R}^{R} e^{-\pi t^2}\,dt = 1$

Therefore, if $\xi \in \mathbb{R}$ :

$\displaystyle e^{-\pi \xi^2} = \int_{-\infty}^{\infty} e^{-\pi x^2} e^{-2\pi i x \xi} \,dx$

We conclude from this post and the previous post that the Gaussian function $e^{-\pi \xi^2}$ is its own Fourier transform.

December 25, 2025
Zeta summation I

The Zeta function is defined in the complex-plan for $Re(z) > 1$ as:

$\displaystyle \zeta(z)=\frac{1}{1^z}+\frac{1}{2^z}+\frac{1}{3^z}+\frac{1}{4^z}+...=\sum_{n=1}^{\infty}\frac{1}{n^z}$

For example:

$\displaystyle \zeta(2)=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...=\frac{\pi^2}{6}$

If we would like to use the Zeta function in order to perform a summation with $Re(z)\leq 1$ we should use the analytic continuation of the Zeta function.

If f(z) is single-valued in some region of the complex-plan, the derivative of $f(z)$ is defined as:

$\displaystyle f'(z)=\lim_{\Delta z\to0}\frac{f(z+\Delta z)-f(z)}{\Delta z}$

If this limit exists we say that $f(z)$ is differentiable at $z$ . If the derivative exists in all points of a region of the complex-plan we say that f(z) is analytic in this region. If the function is analytic inside some circle of convergence $C_0$ it can be represented by the Taylor series:

$\displaystyle a_0+a_1(z-z_0)+a_2(z-z_0)^2+...$

where $z_0$ is the center of the circle $C_0$ . By choosing a new point $z_1$ in $C_0$ which is the center of a new circle $C_1$ the function can be represented by the Taylor series:

$\displaystyle b_0+b_1(z-z_1)+b_2(z-z_1)^2+...$

The figure above illustrates analytic continuation. I like to imagine analytic functions as exquisite porcelain—delicately fragile, yet rigid, able to be extended through analytic continuation.

In order to analytically continue the Zeta function we first consider the following function:

$\displaystyle f(\xi)=e^{-\pi \xi^2}$

where $\xi\in\mathbb{R}$ . We would like to show that this function is equivalent to its Fourier transform

$\displaystyle f(\xi)=e^{-\pi \xi^2}=\int_{-\infty}^{\infty}e^{-\pi x^2}e^{-2\pi i x\xi}\,dx$

if $\xi=0$ :

$\displaystyle f(0)=1=\int_{-\infty}^{\infty}e^{-\pi x^2}\,dx$

if $\xi<0$ :

$\displaystyle \int_{-\infty}^{\infty} e^{-\pi x^2} e^{-2\pi i x \xi}\,dx = \int_{-\infty}^{\infty} e^{-\pi u^2} e^{2\pi i u (-\xi)}\,du = \int_{-\infty}^{\infty} e^{-\pi u^2} e^{-2\pi i u |\xi|}\,du = e^{-\pi \xi^2}$

The demonstration will be completed in the next post.

I wish you a merry Christmas 2025 !

December 18, 2025
Anharmonic oscillator II

Remember that the perturbative series for the anharmonic oscillator is

Anharmonic oscillator I

$\displaystyle E_0(\epsilon) = \frac{1}{2} + \frac{3}{4}\epsilon - \frac{21}{8}\epsilon^2 + \frac{333}{16}\epsilon^3 + \mathcal{O}(\epsilon^4)$

We used Padé approximants to compute the ground state energy $E_0(\epsilon)$ . Now we aim to calculate $E_0(\epsilon)$ using Borel summation. The (formal) Borel sum is given by

$\displaystyle \int_{0}^{\infty} e^{-t} \sum_{n=0}^\infty \frac{a_n}{n!} (\epsilon t)^n \, dt.$

Using the first three coefficients of the perturbative series, the truncated Borel transform is approximated by

$\displaystyle \mathcal{B}E_0(t) \approx \frac{1}{2} + \frac{3}{4} t - \frac{21}{16} t^2,$

so the truncated Borel sum writes

$\displaystyle E_0(\epsilon) \approx \int_0^\infty e^{-t} \left(\frac{1}{2} + \frac{3}{4} \epsilon t - \frac{21}{16} \epsilon^2 t^2 \right) dt = \frac{1}{2} + \frac{3}{4} \epsilon - \frac{21}{8} \epsilon^2.$

since

$\displaystyle \int_0^\infty \frac{1}{2} e^{-t} \, dt = \frac{1}{2}$

$\displaystyle \int_0^\infty e^{-t} \cdot \frac{3}{4} \epsilon \, t \, dt = \frac{3}{4} \epsilon$

$\displaystyle \int_0^\infty e^{-t} \cdot \left( -\frac{21}{16} \epsilon^2 t^2 \right) dt = -\frac{21}{8} \epsilon^2$

This doesn’t really seem like progress, since the first terms of the Borel sum are identical to those of the perturbative expansion. The perturbative expansion $E_0(\epsilon) = \sum_{n=0}^\infty a_n \epsilon^n$ above has coefficients that grow factorially. Bender and Wu showed that for large $n$ ,

$\displaystyle a_n \sim -r\, (-1)^n \left(\frac{3}{2}\right)^n \Gamma\!\left(n+\tfrac12\right), \qquad r>0.$

Since

$\displaystyle \Gamma\!\left(n+\tfrac12\right) \sim n!\, n^{-1/2},$

$formule avec n! en rouge et gras$

thus the series diverges for all $\epsilon \neq 0$ .

Borel summation improves convergence by dividing out this factorial growth.

In summary, even with just a few terms, Borel summation correctly recovers the perturbative results for the anharmonic oscillator then It turns the divergent series into a well-defined and useful result.

December 11, 2025
Borel–Écalle summation

Consider the archetypal divergent series

$\displaystyle \sum_{n=0}^\infty n!\, x^n.$

In a previous post we have seen the Borel summation of $a_1 + a_2 + ... + a_n+ ...$

$\displaystyle \begin{aligned} B &:= \sum_{n=0}^{\infty} \frac{\int_{0}^{\infty} e^{-t}t^{n}dt}{n!} a_n \\ &= \int_{0}^{\infty}e^{-t} \sum_{n=0}^{\infty} \frac{t^n}{n!}a_ndt \end{aligned}$

Step 1 – Ordinary Borel summation

$\displaystyle \sum_{n=0}^{\infty} \frac{t^n}{n!} a_n = \sum_{n=0}^{\infty} \frac{t^n}{n!} n!x^n = \sum_{n=0}^\infty (x t)^n = \frac{1}{1 - x t}$

The ordinary Borel summation fails for $x > 0$ the analytic continuation of $\mathcal{B}(t)$ has a simple pole at $t = 1/x$ lying on the positive real axis. The ordinary Borel integral

$\displaystyle \int_0^\infty e^{-t} \frac{1}{1 - x t}\, dt$

therefore diverges for all $x > 0$ (the pole blocks the integration path).

Step 2 – Borel–Écalle summation
Define the two lateral Borel transforms by deforming the contour slightly above (+) or below (-) the real axis:

$\displaystyle B^\pm(x) = \int_0^{\infty e^{\pm i 0}} e^{-t} \frac{1}{1 - x t}\, dt.$

The notation ∞e^±i0 means that the upper limit of integration is taken to infinity along a ray that approaches the positive real axis from above (angle +0) or from below (angle −0). This slight contour deformation is necessary when the integrand has a singularity (here at t = 1/x) on the positive real axis itself, which would cause the ordinary Borel integral to be ill-defined.

These integrals exist, and

$\displaystyle B^+(x) - B^-(x) = \frac{2\pi i \, e^{-1/x}}{x}.$

The Borel–Écalle summation is defined by

$\displaystyle y(x) := \frac{B^+(x) + B^-(x)}{2}$

And in this case:

$\displaystyle y(x) = -e^{1/x} E_i\!\left(\frac{1}{x}\right)$

where $E_i(z) = \int_z^\infty \frac{e^{-u}}{u}\, du$ is the exponential integral function. Thus, despite the divergence of the original series and the failure of ordinary Borel summation due to the pole on the integration path, the Borel–Écalle median summation recovers the exact analytic continuation on the positive real axis.

December 4, 2025