In the previous post, we introduced Euler summation. The following are two examples where it fails to produce a finite result.
Consider the divergent series:
Define:
The Euler sum is:
Now consider the divergent series:
Define:
The Euler sum is:
Advantages
Regularization of slowly divergent series:
Euler summation can assign a finite value to some divergent series that oscillate or diverge slowly, such as
where 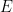 (series) =
(series) =  .
.
Improved convergence:
For many convergent series, Euler transformation accelerates convergence, making it useful for numerical computations.
Analytic continuation link:
It provides a bridge between ordinary summation and more advanced summation methods (e.g. Borel or zeta regularization).
Disadvantages
Limited domain of applicability:
Euler summation fails for series that diverge too rapidly, such as
where 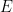 (series) =
(series) =  .
.
Not uniquely defined for all divergent series:
Some series cannot be assigned a finite Euler sum, or the method may yield inconsistent results depending on the transformation order.
Weaker than analytic regularization:
Compared to zeta or Borel summation, Euler’s method handles fewer classes of divergent series and lacks a rigorous analytic continuation framework.
: