Approximaths

Month: October 2025

  • Euler summation I

    So far we’ve seen Padé’s approximants. These have enabled us to approximate a function from its corresponding Taylor series and then transform this (potentially non-convergent) series into a convergent rational fraction.

    We’d like to introduce other techniques that could be used to sum non-convergent series. First, we’ll take a look at Euler summation.

    If the series \sum_{n=0}^{\infty} a_n is algebraically divergent (the terms blow up like some power of n), then the series:

    \displaystyle f(x) = \sum_{n=0}^{\infty}a_n x^n

    converges for x \in (-1,1). If the limit

    \displaystyle E := \lim_{x \to 1_{-}}f(x)

    exists and is finite then it is called the Euler sum E of the original series.

    For example, consider the divergent series:

    \displaystyle 1 - 1 + 1 - 1 + 1 - 1 + ...

    and multiply each n-term with x^n (starting at n = 0):

    \displaystyle f(x) = x^0 - x^1 + x^2 - x^3 + x^4 - x^5 + ...
    \displaystyle = \frac{1}{1-(-x)} = \frac{1}{1+x}
    \displaystyle E = \lim_{x \to 1_{-}}{\frac{1}{1+x}} = \frac{1}{2}

    Therefore (according to Euler summation):

    \displaystyle 1 - 1 + 1 - 1 + 1 - 1 + ... = \frac{1}{2}

  • Padé approximants: Convergence III

    For a function f(z) analytic at z=0, with Taylor series

    \displaystyle f(z) = \sum_{k=0}^{\infty} a_k z^k

    valid within its radius of convergence R, the Padé approximant of order [m/n], denoted \frac{P_m(z)}{Q_n(z)} with \deg P_m \leq m and \deg Q_n \leq n, satisfies

    \displaystyle f(z) - \frac{P_m(z)}{Q_n(z)} = O(z^{m+n+1})

    near z=0. The rational structure of \frac{P_m(z)}{Q_n(z)} allows it to approximate f(z) beyond the disk |z| < R by modeling singularities (e.g., poles or branch points) through the zeros of Q_n(z). This enables analytic continuation into regions where the Taylor series diverges.

    Formally, for a meromorphic function f(z) in a domain D, the diagonal Padé approximants [n/n] often converge to f(z) in D \setminus S, where S is the set of poles of f:

    Let f(z) be meromorphic in a domain D \subseteq \mathbb{C}, with a set of poles S of finite total multiplicity. The diagonal Padé approximants [n/n], defined as rational functions \frac{P_n(z)}{Q_n(z)} satisfying

    \displaystyle f(z) - \frac{P_n(z)}{Q_n(z)} = O(z^{2n+1})

    near z=0, converge uniformly to f(z) on compact subsets of D \setminus S as n \to \infty.

    The zeros of Q_n(z) approximate the poles in S, enabling analytic continuation of f(z) beyond the radius of convergence of its Taylor series.

  • Nuttall’s Padé approximant

    Let f(z) = \sum_{k=0}^\infty C_k z^k be a power series. The denominator Q_{n-1}(z) of the Padé approximant P(n, n-1) is given by Nuttall’s compact form:

    \displaystyle Q_{n-1}(z) = \frac{ \begin{vmatrix} C_0 & C_1 & C_2 & \cdots & C_{n-1} & C_n \\ C_1 & C_2 & C_3 & \cdots & C_n & C_{n+1} \\ C_2 & C_3 & C_4 & \cdots & C_{n+1} & C_{n+2} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ C_{n-2} & C_{n-1} & C_n & \cdots & C_{2n-3} & C_{2n-2} \\ 1 & z & z^2 & \cdots & z^{n-2} & z^{n-1} \end{vmatrix} }{ \begin{vmatrix} C_0 & C_1 & C_2 & \cdots & C_{n-1} \\ C_1 & C_2 & C_3 & \cdots & C_n \\ C_2 & C_3 & C_4 & \cdots & C_{n+1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ C_{n-1} & C_n & C_{n+1} & \cdots & C_{2n-1} \end{vmatrix} }

    The numerator P_n(z) is obtained by satisfying the Padé approximation condition: f(z) Q_{n-1}(z) - P_n(z) = O(z^{2n}).

    The compact form of Nuttall’s Padé approximant P(n, n-1) is particularly valuable in numerical analysis and theoretical physics for its efficiency in computing Padé approximants without explicitly solving large linear systems.

    By expressing the denominator Q_{n-1}(z) as a ratio of determinants, it provides a direct and elegant method to capture the approximant’s poles, which is crucial for analyzing singularities of functions, especially in Stieltjes series or meromorphic functions.

    This formulation simplifies calculations, facilitates the study of convergence properties, and connects Padé approximants to orthogonal polynomials, enabling applications in areas like quantum field theory and asymptotic analysis where rapid computation and singularity detection are essential.

  • Continued fractions II

    A well-known continued fraction representation of exp(x) is:

    \displaystyle exp(x) = 1 + \frac{x}{1 - \frac{x}{2 + \frac{x}{3 - \frac{x}{4 + \cdots}}}}

    Using the procedure described in the previous post, we can show that the near-diagonal Padé coefficients presented in this post can be converted to a sequence of truncated fractions corresponding to the continued fraction above (see figures below).

    …

    P(m,n) 0 1 2 3
    0
    \displaystyle 1
    \displaystyle 1 + x
    		 …
    1
    \displaystyle 1 + \cfrac{x}{1 - \cfrac{x}{2}}
    \displaystyle 1 + \cfrac{x}{1 - \cfrac{x}{2 + \cfrac{x}{3}}}
    		 …
    2
    \displaystyle 1 + \cfrac{x}{1 - \cfrac{x}{2 + \cfrac{x}{3 - \cfrac{x}{4}}}}
    \displaystyle 1 + \cfrac{x}{1 - \cfrac{x}{2 + \cfrac{x}{3 - \cfrac{x}{4 + \cfrac{x}{5}}}}}
    		 …
    3 …
    … … … … … …

    Caption: Padé Approximants P(m,n) for exp(x) expressed as continued fractions.

    The relationship between Padé approximants and continued fractions is a profound connection in mathematical analysis, particularly for approximating functions like exp(x). Padé approximants, which are rational functions that match the Taylor series of a function up to a specified order, can often be expressed as continued fractions. This representation is advantageous because continued fractions can provide better convergence properties for certain functions, especially near singularities. For instance, the near-diagonal Padé approximants for exp(x), as shown above, can be systematically converted into a sequence of truncated continued fractions, revealing a structured pattern known as the “main Padé sequence.”

    A function with a convergent Taylor series around 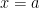x = a can be approximated by a sequence of diagonal Padé approximants P(n,n)(x) = \frac{P_n(x)}{Q_n(x)}, provided the associated Hankel matrices H_n, built from the Taylor coefficients, have nonzero determinants.

    When this “Padé table” is normal (i.e., \det(H_n) \ne 0 for all n), each Padé approximant is uniquely defined.

    Under these conditions, one can systematically derive a continued fraction whose successive convergents exactly match the Padé approximants.

    This establishes a rigorous connection between the Taylor series, Padé approximation, and continued fraction representation of the function.

  • Continued fractions I

    We can use Padé approximants to build a sequence of truncated continued fractions representing a given function. For example using P(1,1):

    P(1,1) = \frac{A_0 + A_1 x}{1 + B_1 x} = C_0 + C_1 x + C_2 x^2

    Solving the linear systems presented in post Computing Padé approximants sequentially leads to:

    C_1 B_1 = - C_2 \quad \Rightarrow \quad B_1 = -\frac{C_2}{C_1}
    \begin{pmatrix} C_0 & 0 \\ C_1 & C_0 \end{pmatrix} \begin{pmatrix} 1 \\ B_1 \end{pmatrix} = \begin{pmatrix} A_0 \\ A_1 \end{pmatrix}
    A_0 = C_0, \quad A_1 = C_1 + C_0 B_1

    Setting C_0 = 1:

    P(1,1) = \frac{1 + (C_1 + B_1) x}{1 + B_1 x}
    P(1,1) = \frac{1 + (C_1 - \frac{C_2}{C_1}) x}{1 - \frac{C_2}{C_1} x}
    P(1,1) = \frac{1 + (C_1 - \frac{C_2}{C_1}) x}{1 + (C_1 - \frac{C_2}{C_1}) x - C_1 x}
    P(1,1) = \frac{1}{1 - \frac{C_1 x}{1 + (C_1 - \frac{C_2}{C_1}) x}}
    P(1,1) = \frac{1}{1 - \frac{C_1 x}{1 - (\frac{C_2}{C_1} - C_1) x}}

    Now define:

    \frac{b_0}{1 - \frac{b_1 x}{1 - b_2 x}} = \frac{1}{1 - \frac{C_1 x}{1 - \left(\frac{C_2}{C_1} - C_1\right) x}}

    We have:

    b_0 = 1, \quad b_1 = C_1, \quad b_2 = \frac{C_2}{C_1} - C_1, \quad \ldots